¿Qué es un circuito RLC?
Un circuito RLC es un tipo de circuito eléctrico compuesto por tres elementos básicos: un resistor (R), un inductor (L) y un condensador (C). El resistor disipa energía en forma de calor y tiene valores típicos entre 1 Ω y 10 kΩ. El inductor, que almacena energía en un campo magnético, suele tener valores de inductancia entre 1 mH y 10 H. Por su parte, el condensador, que almacena energía en un campo eléctrico, presenta capacidades que oscilan entre 1 µF y 1 mF. Estos componentes pueden conectarse en serie, donde la corriente es la misma para todos, o en paralelo, compartiendo el voltaje. Su comportamiento se modela mediante las leyes de Kirchhoff: la ley de corrientes para la configuración paralela y la ley de tensiones para la serie. Además, las ecuaciones diferenciales permiten analizar fenómenos como la oscilación y la resonancia en estos circuitos.
Componentes principales:
- Resistor (R): Limita el flujo de corriente y disipa energía como calor.
- Inductor (L): Almacena energía en un campo magnético.
- Condensador (C): Almacena energía en un campo eléctrico.
La resonancia en circuitos RLC
La resonancia ocurre cuando la frecuencia de la fuente aplicada coincide exactamente con la frecuencia natural del circuito, un fenómeno crucial en sistemas eléctricos y electrónicos. En este estado, las reactancias inductiva y capacitiva se anulan mutuamente, dejando al circuito con una impedancia mínima en configuración serie o una impedancia máxima en configuración paralelo. Esto permite que la corriente alcance su valor máximo en un circuito en serie, lo que es esencial en aplicaciones como transmisores de radio y filtros selectivos. En el caso de un circuito en paralelo, la resonancia produce un aumento significativo de la tensión en los elementos del circuito, utilizado frecuentemente en resonadores de antenas y sintonizadores. Este equilibrio entre componentes reactivos hace que la resonancia sea una herramienta indispensable para optimizar el rendimiento y la eficiencia en una variedad de sistemas electrónicos.
Frecuencia de resonancia:
La frecuencia de resonancia (f_r) se calcula utilizando la siguiente fórmula:
f_r = \frac{1}{2\pi\sqrt{LC}}
donde:
Les la inductancia en henrios (H).Ces la capacitancia en faradios (F).
Ejemplo práctico:
Supongamos un circuito RLC en serie con:
R = 10 \OmegaL = 50 \text{mH}C = 100 \mu\text{F}
La frecuencia de resonancia es:
f_r = \frac{1}{2\pi\sqrt{50 \times 10^{-3} \times 100 \times 10^{-6}}} \approx 225 \text{Hz}
Comparación entre configuraciones serie y paralelo
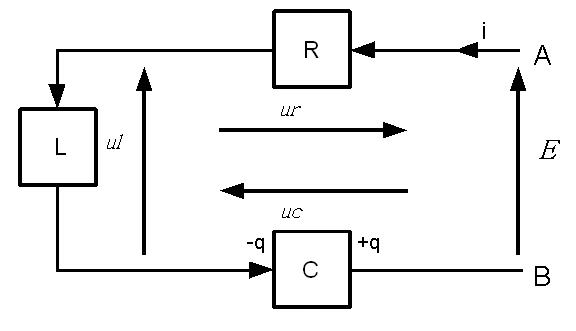
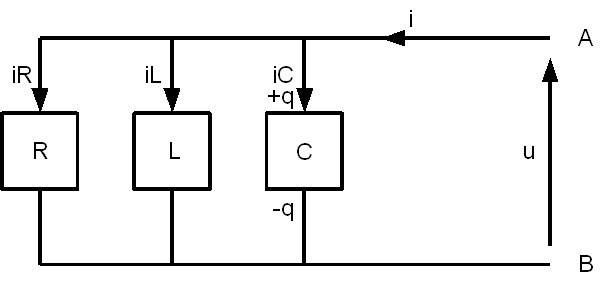
| Característica | Serie | Paralelo |
|---|---|---|
| Impedancia en resonancia | Mínima | Máxima |
| Corriente en resonancia | Máxima | Mínima |
| Aplicaciones típicas | Filtros pasa banda | Filtros rechazo de banda |
Aplicaciones de los circuitos RLC
Los circuitos RLC tienen numerosas aplicaciones en el campo de la ingeniería y la electrónica. Algunos ejemplos incluyen:
- Radios: Sintonización de estaciones mediante resonancia.
- Filtros: Diseño de filtros pasa banda y rechazo de banda.
- Sistemas de potencia: Compensación de factor de potencia en sistemas AC.
En conclusión, los circuitos RLC desempeñan un papel fundamental en diversas aplicaciones dentro de la ingeniería y la electrónica, gracias a sus propiedades únicas de resonancia y respuesta a la frecuencia. En el ámbito de las radios, estos circuitos son esenciales para la sintonización de estaciones, permitiendo captar señales específicas mediante el ajuste de la frecuencia resonante. De igual manera, en el diseño de filtros, los circuitos RLC son empleados en la creación de filtros pasa banda y de rechazo de banda, fundamentales en sistemas de comunicaciones y procesamiento de señales, para seleccionar o eliminar frecuencias no deseadas. Además, en los sistemas de potencia, los circuitos RLC son clave en la compensación del factor de potencia, especialmente en sistemas de corriente alterna, optimizando la eficiencia y reduciendo las pérdidas de energía. Gracias a estas aplicaciones, los circuitos RLC siguen siendo una herramienta esencial en la tecnología moderna, mejorando el rendimiento y la calidad en numerosos dispositivos electrónicos y sistemas de comunicación. Su versatilidad y eficiencia continúan impulsando avances significativos en diversas áreas de la electrónica y la ingeniería.
