2e partie? : Améliorer l’intégrité des signaux
Par Richard Anslow, System Applications Manager (Analog Devices), et Sylvain Le Bras, Field Applications Engineer (Würth Electronik)
Comment utiliser LTspice pour simuler la compatibilité électromagnétique et l’intégrité du signal
Ce document constitue le deuxième d’une série de trois articles qui présentent des modèles de simulation de la compatibilité électromagnétique (CEM) et d’intégrité du signal sous LTspice®. Dans le premier article intitulé «?Compatibilité électromagnétique?: optimiser la simulation avec LTspice?», nous avons étudié les outils de simulation LTspice pour les composants d’alimentation électrique, les émissions conduites et l’immunité aux interférences électromagnétiques.
Dans ce deuxième volet, nous verrons comment l’association de LTspice et de programmes rédigés en langage C peut aider les concepteurs à comprendre et à améliorer l’intégrité des signaux sur les réseaux filaires. Ces outils leur permettront notamment d’éviter de multiples itérations de test en laboratoire, ainsi que d’onéreuses reprises au niveau matériel. Des modèles de simulation sont fournis pour valider la conformité aux normes et standards de communications par bus de terrain (RS-485, RS-232), au protocole de transmission en fond de panier à haut débit (LVDS), à l’omniprésente norme USB, et au nouveau standard Ethernet à paire unique (SPE) qui permet d’alimenter des appareils à travers la ligne de données (PoDL).
Pourquoi les concepteurs doivent-ils se préoccuper de l’intégrité des signaux??
L’intégrité des signaux dépasse le simple cadre de la mise en œuvre d’une liaison opérationnelle pour votre prototype. Même si votre liaison semble fonctionner, il est recommandé de procéder à une vérification approfondie de la qualité du signal et ce, pour trois raisons?:
• la fiabilité?: la distance, le débit et l’environnement peuvent accroître le taux d’erreurs binaires (BER) et atteindre des valeurs inacceptables pour les mécanismes de correction d’erreurs du système?;
• la conformité aux normes IEEE?: la conformité aux recommandations de l’IEEE est la garantie d’interactions transparentes entre les éléments du réseau ;
• la conformité aux directives de compatibilité électromagnétique?: une vitesse de balayage (slew rate) élevée et des dépassements de tension (overshoots) sont souvent à l’origine de non-conformités en raison de leur contenu harmonique élevé.
Résoudre les problèmes d’intégrité du signal en utilisant LTspice
Dans cet article, nous tenterons de répondre aux questions suivantes?:
• Est-ce que mon système est capable d’assurer l’intégrité des signaux requise??
• Quel aspect du signal dois-je améliorer en priorité : la vitesse de balayage (slew rate), l’ondulation (ringing), la gigue (jitter) ou l’adaptation (matching)??
• Mon système est opérationnel, mais continuera-t-il à fonctionner avec fiabilité au fil du temps, en fonction de la température et de la tolérance des différents composants??
Après avoir lu cet article, vous pourrez?:
• procéder à l’analyse d’intégrité du signal dans LTspice ;
• générer, importer et utiliser des vecteurs de test représentatifs pour produire une analyse et un graphique similaire à la figure?1;
• effectuer une validation statistique de votre système sur plusieurs paramètres aléatoires.
Effectuer une simulation du diagramme de l’œil
Le diagramme de l’œil (eye diagram) est un moyen pratique d’évaluer la conformité d’un signal côté émetteur ou récepteur. Le diagramme de l’œil est une représentation temporelle du signal.
Cette représentation utilise la persistance pour analyser un grand nombre de symboles et vérifier que le niveau, la gigue et le temps de montée des signaux sont appropriés.
LTspice propose certains des outils nécessaires pour procéder à une analyse du diagramme de l’œil. Pour effectuer une analyse complète, plusieurs étapes supplémentaires doivent toutefois être mises en œuvre.
Générer un fichier PWL avec votre vecteur de test
LTspice propose un moyen efficace d’appliquer un vecteur de test dans votre simulation. Il est nécessaire de « lire » une grande quantité de données pour couvrir une situation pouvant donner lieu à des non-conformités.
Certaines non-conformités peuvent apparaître dans des situations particulières?:
• de longues séries de bits consécutifs ;
• des séquences équilibrées non nulles ;
• un phénomène de diaphonie lié à la proximité d’autres canaux de transmission.
En d’autres termes, si les données sont générées à l’aide d’une fonction aléatoire, vous devrez peut-être utiliser des milliers de symboles pour avoir la certitude de rencontrer une série de 11 bits consécutifs de haut niveau.
Le format de données PWL attendu par LTspice est représenté à la figure?2.

Où?:
• la première valeur est le temps ;
• la deuxième valeur est la sortie (tension, courant, température, etc.) ;
• -> est le caractère de tabulation (code Ascii #09) ;
• CR est le caractère Retour Chariot (Carriage Return) (code Ascii #13) ;
• et LF le caractère de saut de ligne (Line Feed) (code Ascii #10)

De nombreuses options peuvent être utilisées pour générer des vecteurs de test. Dans le cadre de nos simulations, nous avons choisi le langage de programmation C.
Quelques lignes de code suffisent pour générer facilement de grands vecteurs de test prêts à être injectés dans la simulation. La figure?3 représente un extrait du code utilisé pour générer le vecteur de test, et la figure?4 la forme d’onde générée par le programme C.
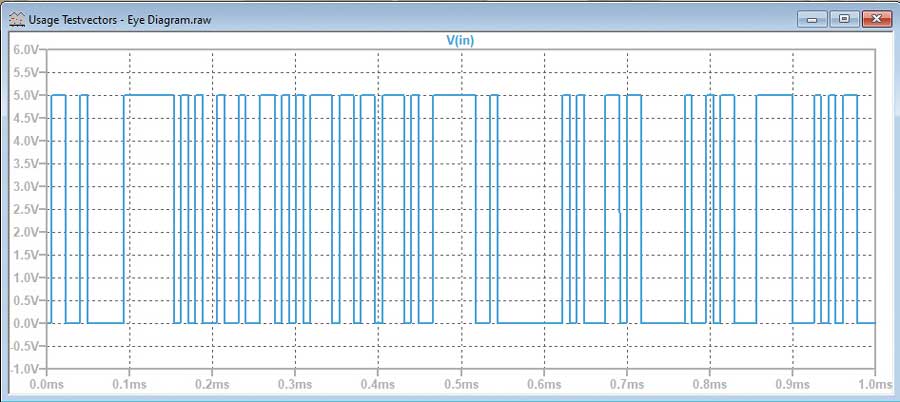
Les concepts utilisés dans les communications filaires tels que le remplissage de bits (bit stuffing) peuvent être mis en œuvre avec quelques lignes de code (figure?5).

Générer un fichier PWL avec un vecteur de test capturé
Il est également possible d’utiliser des données réelles et de les importer dans LTspice. Une fois acquises avec votre matériel de laboratoire habituel, quelques étapes suffisent pour importer les données.
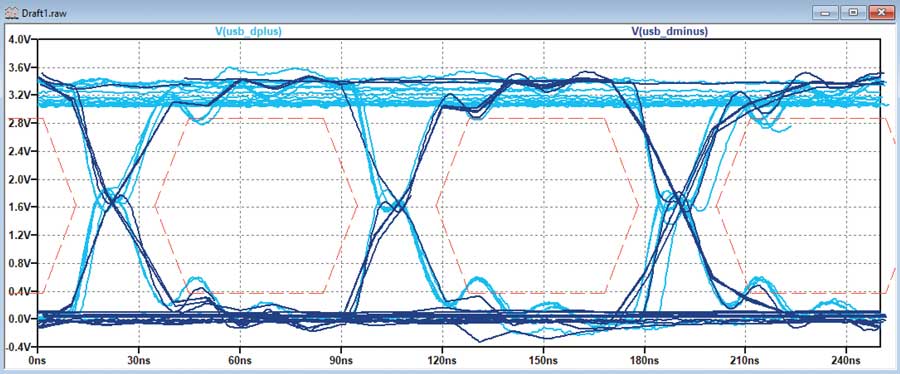
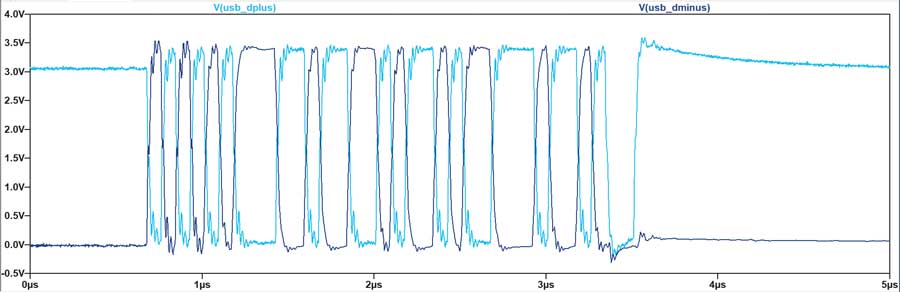
À titre d’exemple, la figure?6 représente la capture d’une communication USB 1.0 réalisée avec un oscilloscope.
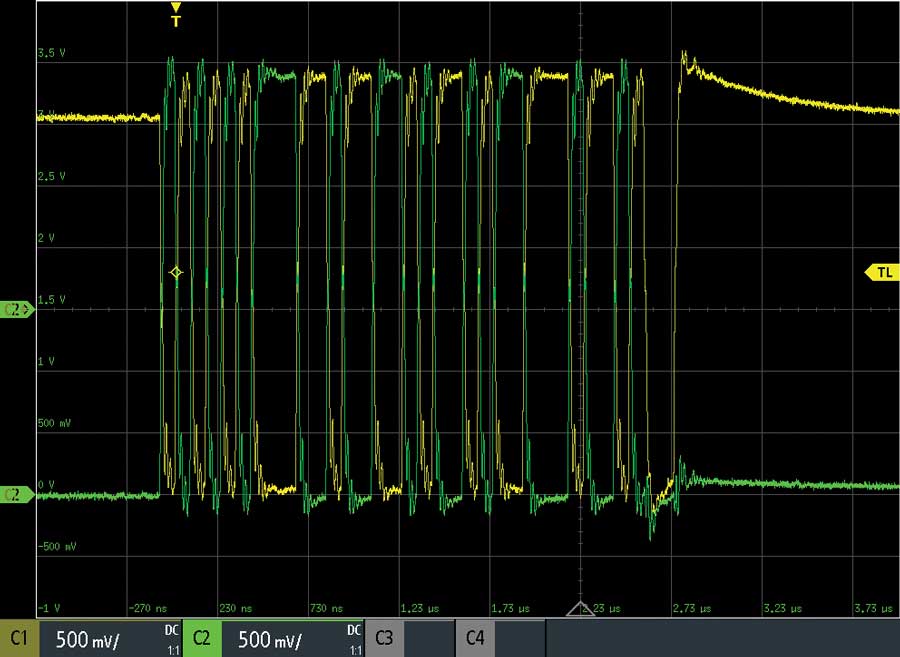
La figure?7 est l’exemple typique d’un ensemble de données sauvegardé par un oscilloscope. Si le format exact peut varier, les règles fournies pour importer les données dans LTspice restent applicables.
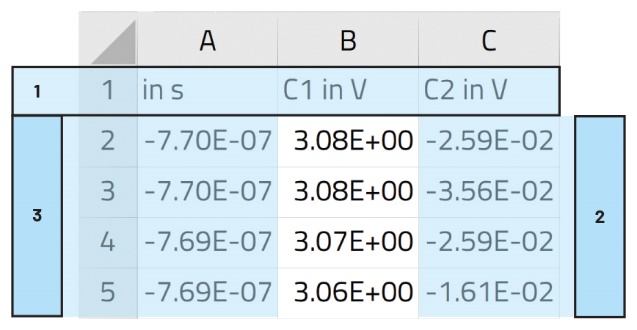
Pour utiliser cet ensemble de données dans une simulation LTspice, quelques modifications s’imposent ?:
1. la ligne d’en-tête doit être supprimée ;
2. une seule colonne de données doit être présente dans le fichier PWL fourni à LTspice ;
3. les valeurs temporelles doivent exclusivement être positives.
Vos données peuvent alors être utilisées dans LTspice.
Utilisation du fichier PWL d’un vecteur de test
Pour utiliser le fichier PWL généré, vous pouvez ajouter une source de tension et un chemin de fichier à votre projet (figure?9).
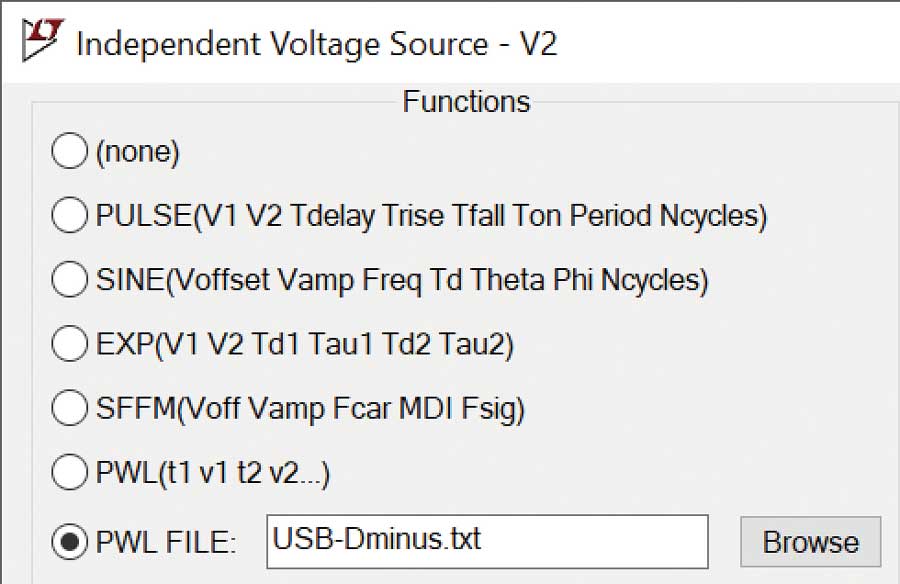
Les chemins d’accès absolus et relatifs fonctionneront, mais il est recommandé d’utiliser des chemins d’accès relatifs pour pouvoir partager la simulation avec vos collègues.

Activation et réglage de la fonction de diagramme de l’œil
Pour bénéficier pleinement du potentiel de cette fonctionnalité enfouie de LTspice, vous devrez d’abord exécuter la simulation.
Une fois la simulation effectuée et les signaux affichés, effectuez un clic droit avec la souris sur l’axe horizontal (temps).
Une boîte de dialogue affiche le bouton du diagramme de l’œil (figure?12).
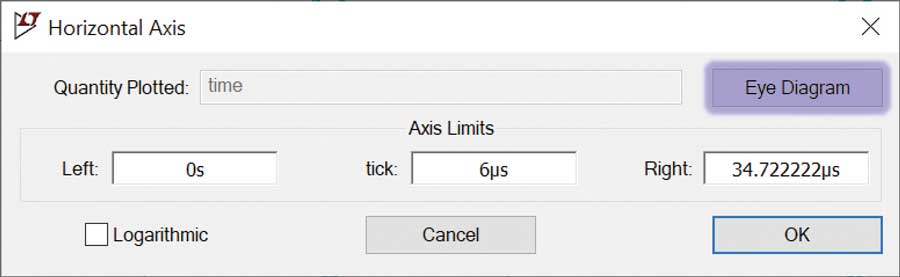
Cette fenêtre contextuelle permet d’activer et de régler l’affichage du diagramme de l’œil au moyen de paramètres explicites.
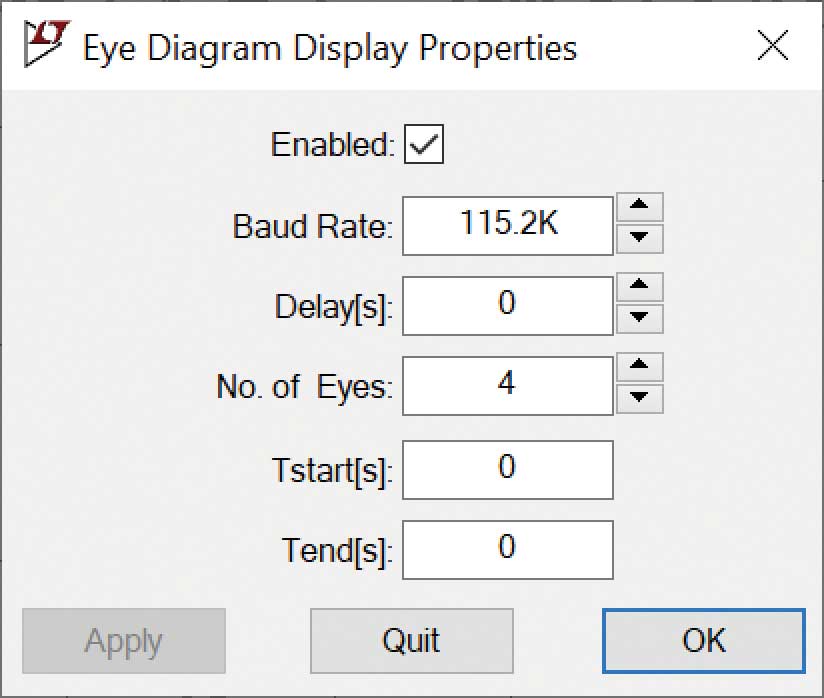
Après validation, l’affichage ressemblera à la figure?14.
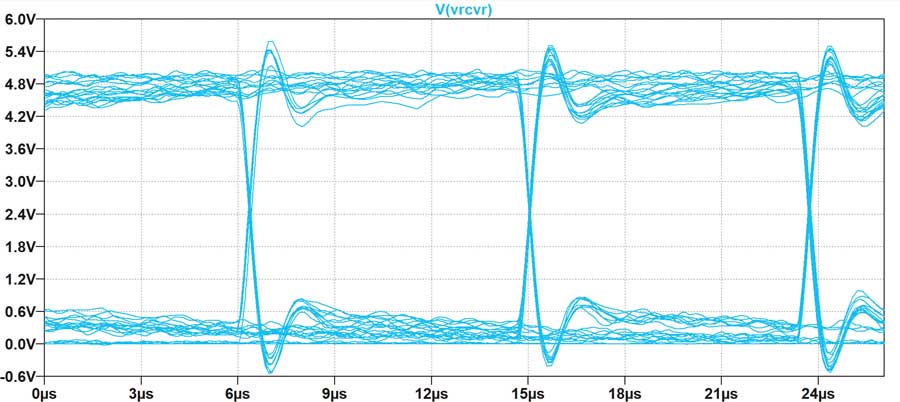
Calcul et affichage du masque du diagramme de l’œil
Pour simplifier l’évaluation de l’intégrité d’un signal, on associera le diagramme de l’œil à un masque. Ce masque oculaire n’est pas une fonction standard de LTspice, mais il est toujours possible de l’implémenter (de même que la ligne indiquant la limite des émissions conduites dans l’article 1).
La spécification du diagramme de l’œil est standard, de sorte que la majeure partie du masque peut être évaluée à partir d’un ensemble de variables réduit (figure?15).
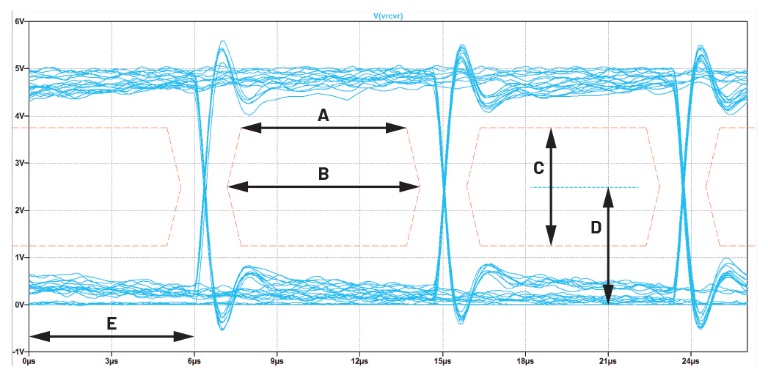
La liste suivante définit les lettres A à E utilisées dans le masque du diagramme de l’œil?:
• A?: largeur à plat (eye flat width) : peut être nulle dans certaines définitions de masque ;
• B?: largeur de l’œil (eye width) : essentielle pour évaluer plusieurs paramètres tels que la gigue maximale, la vitesse de balayage ou la vitesse de transmission ;
• C?: hauteur de l’œil (eye height) : cette valeur peut différer selon que ce paramètre est évalué à l’extrémité proche ou lointaine du câble ;
• D?: centre de l’œil (eye center) : définit la tension centrale de l’œil ;
• E?: retard (delay) : ce paramètre est exclusivement utilisé dans LTspice pour déplacer le signal dans la fenêtre de tracé.
Générer un masque du diagramme de l’œil
Dans le premier article de cette série, nous avons décrit comment les éléments de dessin peuvent être utilisés pour afficher les lignes de limite des émissions conduites dans un spectre FFT. Dans ce deuxième volet, nous expliquons comment utiliser ces mêmes outils pour dessiner un masque du diagramme de l’œil.
La génération du diagramme de l’œil est une opération plus complexe que la génération et l’ajout d’une ligne de limite des émissions conduites. Pour les diagrammes de l’œil, nous utilisons une page Web avec JavaScriptP2 pour générer la définition du diagramme de l’œil, qu’il sera ensuite possible de coller dans le fichier Plot Setting (*.plt) de l’affichage de signal dans LTspice. Ce programme JavaScript (figure?16) peut être utilisé par le concepteur pour compléter son projet.
Dans le cas des standards d’interfaces câblées courants, les définitions des diagrammes de l’œil sont déjà préréglées. En cliquant sur chaque bouton, les champs sont renseignés automatiquement avec des valeurs typiques.

Il est également possible d’affiner ou d’implémenter votre propre définition en utilisant les champs fournis.

Les commandes de paramétrage de tracé correspondantes sont générées en cliquant sur le bouton Update (mise à jour). Ces lignes peuvent être ajoutées à votre fichier Plot Setting (paramètres de tracé) en utilisant la méthode décrite dans notre premier article.
Il peut s’avérer nécessaire d’ajuster le nombre d’yeux à dessiner et le délai LTspice pour optimiser l’affichage (figure?19).
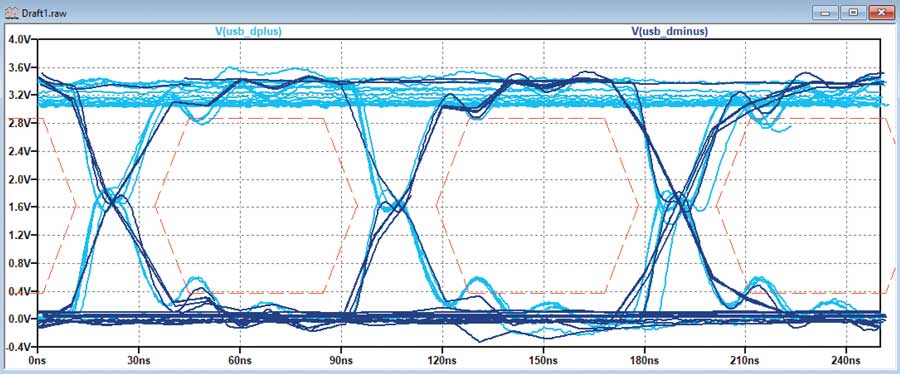
Évaluation de la conformité dans une plage de tolérances
Les composants utilisés dans nos projets de conception affichent de larges tolérances, des calculs nous permettant de vérifier si ces tolérances sont susceptibles d’occasionner des problèmes. Mais lorsqu’un design comprend plusieurs centaines de composants, les approches manuelles (manuscrites ou sur tableur) s’avèrent fastidieuses et risquent de ne pas tenir compte de paramètres importants. Il est possible d’utiliser des tolérances réduites pour certains composants, mais l’utilisation exclusive de composants à faible tolérance entraînera des problèmes de prix et de disponibilité, sans oublier les effets du vieillissement ou de la dépendance vis-à-vis de la température.
Pour valider une conception en fonction de ses tolérances, le logiciel Spice et, par extension, LTspice, bénéficient de plusieurs outils étonnants.
Les chapitres suivants présentent les techniques d’analyse des tolérances à l’aide des distributions de Monte-Carlo et gaussienne, ainsi que l’analyse pire cas (APC) dans LTspice.
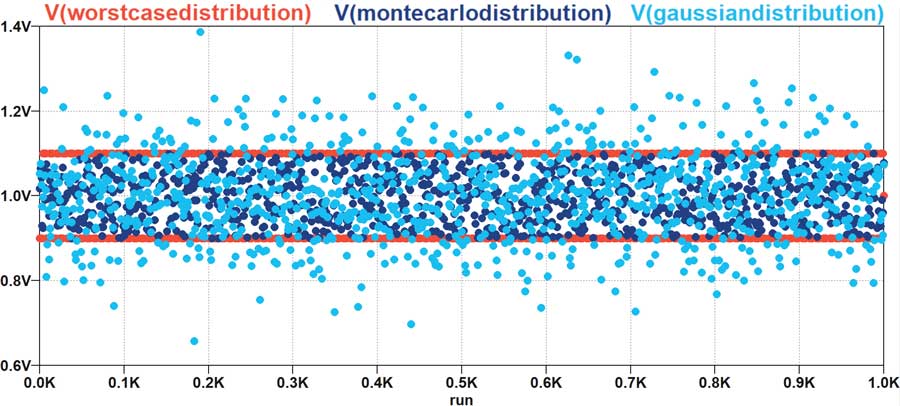
Circuit de test commun pour les distributions gaussienne, pire cas et Monte-Carlo
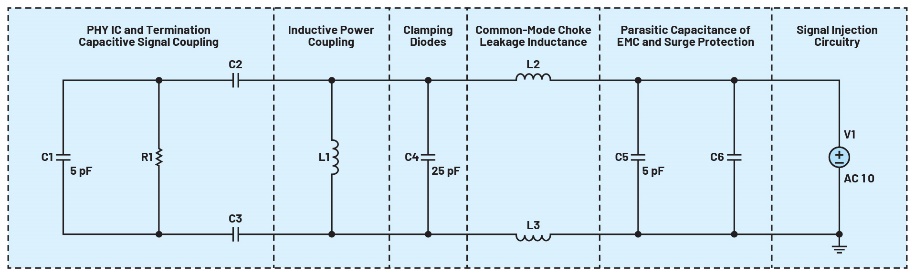
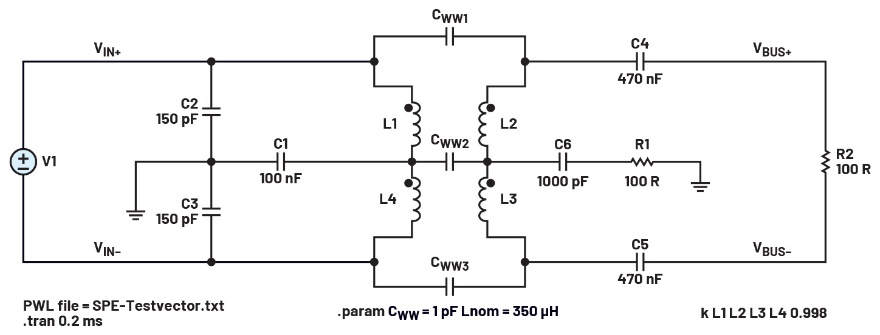
Pour comparer la pertinence et l’exhaustivité dans un scénario réel, nous avons choisi l’exemple suivant, basé sur les travaux de Steffen Graber4?: cette configuration représente un circuit de simulation pour la couche physique de la norme SPE 10Base-T1L (10SPE) ou MDI.
Le circuit de simulation illustré à la figure?21 inclut une résistance de terminaison de 100 ? (±10 %) pour les émetteurs PHY/MAC-PHY Ethernet 10BASE-T1L ADIN1110 ou ADIN1100 d’Analog Devices.
La capacité de couplage du signal, les inductances de couplage, la bobine de mode commun et d’autres composants de protection CEM sont modélisés. Pour certains composants, la valeur recommandée et la plage de tolérance sont ajoutées.
La syntaxe du tracé de la perte de retour est la suivante?:
(100+1/I(V1))/(100-1/I(V1))
Simulation de Monte-Carlo
Une simulation Monte-Carlo extrait une valeur aléatoire dans la plage de tolérance de chaque composant spécifié dans le circuit de simulation. Toutes les valeurs comprises dans la plage de tolérance du composant affichent une probabilité égale pour la simulation du circuit.
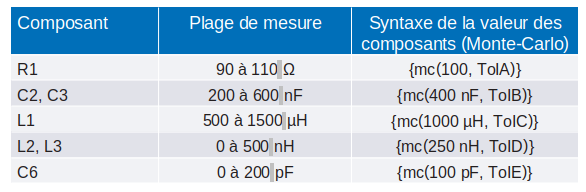
LTspice inclut une fonction Monte-Carlo intégrée très pratique dotée d’une syntaxe simple. Prenons un exemple : pour créer une résistance de 100 ? avec une tolérance de 10 %, on utilisera la syntaxe suivante?:
{mc(100R, ToIA)}
.param ToIA = 0.10
Tableau 1. Définition des valeurs et des tolérances des composants avec la méthode Monte-Carlo
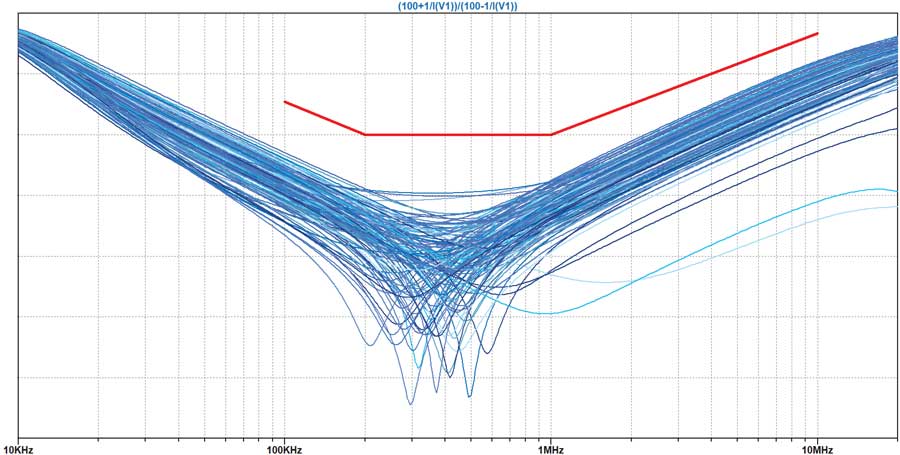
Le circuit décrit à la figure?214 peut être utilisé pour simuler les pertes de retour, une mesure de toutes les réflexions de signal susceptibles de se produire.
Les pertes de retour sont provoquées par des défauts d’adaptation d’impédance en tous points d’une liaison par câble. Exprimées en décibels, elles représentent un enjeu particulier pour les communications à haut débit ou longue distance (câbles de1 700 mètres) correspondant au protocole 10BASE-T1L.
Pour ajouter la ligne de limite des pertes de retour MDI à votre tracé (ligne rouge à la figure?23), cliquez sur Save Plot Settings (Enregistrer les paramètres de tracé) dans le menu Plot Settings (Paramètres de tracé).
Ouvrez le fichier .PLT à l’aide d’un éditeur de texte, avant de copier-coller la syntaxe de définition de ligne comme indiqué dans le fichier Excel (figure?22).

Pour obtenir des valeurs identiques dans vos simulations, effectuez un clic droit sur la forme d’onde, puis cliquez sur le bouton Don’t Plot Phase (Ne pas tracer la phase).
Conclusion sur la simulation de Monte-Carlo
La simulation de Monte-Carlo constitue un moyen efficace d’évaluer la conformité d’une conception électronique dans sa plage de tolérance ; à ce titre, elle répond aux besoins de la plupart des concepteurs tout en maintenant le nombre de simulations à un niveau raisonnable.
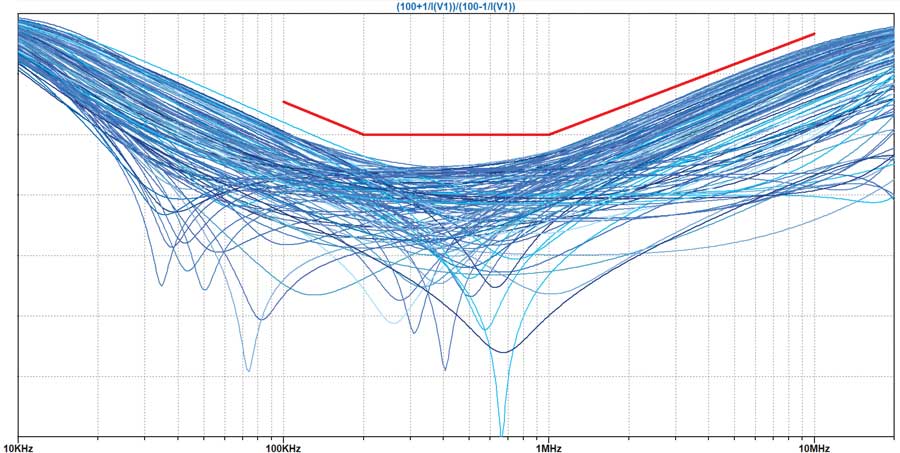
Simulation pire cas
La fonction de simulation pire cas (« worst-case ») n’est pas intégrée à LTspice. Vous pouvez toutefois implémenter des fonctions pour simuler les pires cas, comme l’expliquent Joseph Spencer et Gabino Alonso dans leurs travaux.2
Les fonctions .func binary(run,index) et .func wc(nom,tol,index) sont nécessaires pour effectuer des simulations selon la méthode pire cas ; à ce titre, elles doivent être placées dans votre feuille de schéma LTspice en tant que directive SPICE.
.func binary(run,index) floor(run/(2**index))-2*floor(run/(2**(index+1)))
.func wc(nom,tol,index) if(run==numruns,nom,if(binary(run,index),nom*(1+ tol),nom*(1-tol)))
Pour utiliser ces fonctions, vous devez?:
• déclarer le nombre de simulations nécessaires pour couvrir les valeurs maximales, minimales et nominales de chaque composant soumis à l’analyse pire cas spécifiée à l’aide d’instructions numruns. Le nombre d’exécutions est déterminé par 2N+1, où N est égal au nombre d’indices différents liés aux tolérances des composants. En figure?21, ce nombre est de 129 (y compris l’exécution « 0 »), de sorte que la syntaxe est la suivante?:
.param numruns = 129
• au lieu de la valeur ordinaire du composant, vous devez déclarer l’expression suivante?:
{wc(100R, 0.1, 0)}
Où?:
• 100R est la valeur nominale ;
• 0,1 est la tolérance (+/- 10 % ici) ;
• 0 est l’indice du paramètre à faire varier ; le composant suivant prend l’indice 1.
Exécutez le circuit de simulation représenté à la figure?21 en utilisant les expressions du tableau suivant au lieu des valeurs statiques?:
Tableau 2. Définition des valeurs et tolérances des composants avec la méthode pire cas
Les résultats sont affichés dans le tracé de la forme d’onde à la figure?24.
La ligne limite du masque pour les pertes de retour MDI est ajoutée en éditant le fichier Plot Settings comme décrit précédemment.
Conclusion sur l’analyse pire cas
Steve Knudtsen propose une synthèse3 des avantages et des limites inhérentes à l’utilisation de l’analyse pire cas pour la conception de systèmes.
Cette méthode d’analyse est une approche courante où les paramètres des composants sont ajustés selon leur limite de tolérance maximale.
Parmi les limites de cette approche figurent les résultats qui ne correspondent pas aux résultats couramment observés?: pour observer un système présentant les performances pire cas, il est nécessaire d’assembler un très grand nombre de systèmes.
Or, si les systèmes sont conçus pour les pires cas, la sélection des composants risque d’être très onéreuse.
Toutefois, l’association de cette méthode et des méthodes de Monte-Carlo ou gaussienne peut fournir des informations précieuses sur le système.
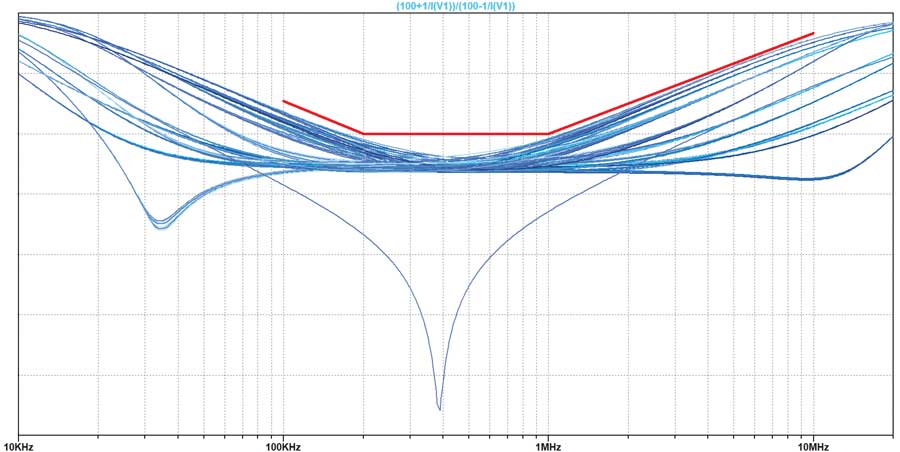
L’analyse pire cas convient aux validations comportementales brutes lorsque les simulations sont très longues et que le comportement nominal est déjà validé.
Simulation gaussienne
Le logiciel LTspice intègre une fonction gaussienne ; lorsque les valeurs centrées affichent une probabilité de survenue plus élevée, sa syntaxe est simple :
{valeur_nominale*(1+gauss(tolérance/?))}
Les ajustements effectués par rapport au paramètre d’écart-type ? de la distribution gaussienne peuvent être effectués à l’aide des expressions suivantes du tableau 3.
Tableau 3. Définition de la valeur et des tolérances des composants avec la méthode de la distribution gaussienne
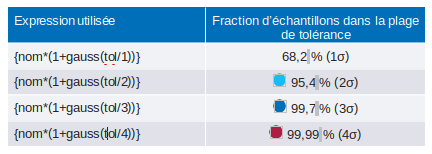
Ou, en utilisant une représentation plus graphique?:
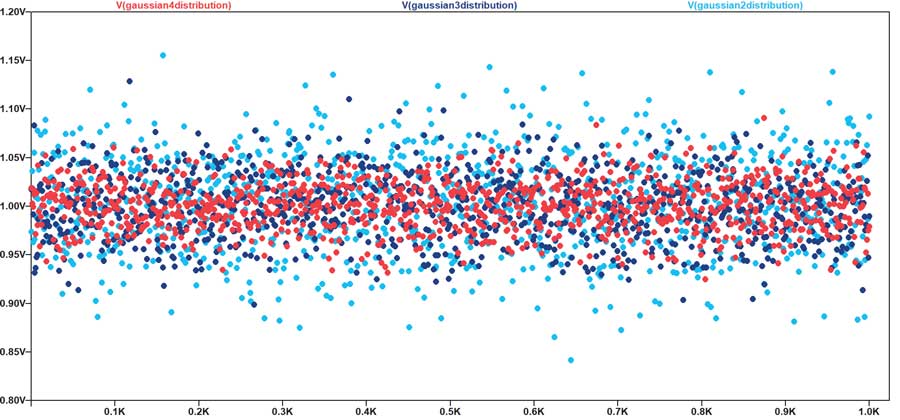
Par exemple, pour créer une résistance de 100 ? avec une tolérance de 10 % et une probabilité de valeur de 4 ? dans la tolérance, on utilisera la syntaxe suivante?:
{100R*(1+gauss(ToIA/4))}
.param ToIA = 0,10
La figure?26 indique le résultat de 128 exécutions de la simulation fournie à la figure?19 avec la simulation gaussienne de la figure?19 et les paramètres de la distribution gaussienne pour une probabilité de 4 ?.
Conclusion sur la méthode de distribution gaussienne
La méthode gaussienne constitue dans de nombreux cas la meilleure manière de simuler les variations d’une conception électronique.
La distribution gaussienne des paramètres autour d’une valeur nominale demeure la manière la plus naturelle d’étudier les répercussions des tolérances.
Malheureusement, cette approche a un coût. Pour qu’elle soit exhaustive, il est nécessaire de procéder à un nombre élevé de simulations.
Cette distribution choisit également des valeurs en dehors de la plage de tolérance, sans tenir compte des opérations de tri (sorting) et de classification sélective (binning) effectuées par les fabricants de composants électroniques.
Application à l’analyse d’une liaison 10BASE-T1L
Il est possible de remplacer plusieurs bus de terrain en utilisant la norme Ethernet 10BASE-T1L. En effet, un même câble peut servir à la fois pour le bus de terrain traditionnel et pour le bus 10BASE-T1L, qui est en fait une simple paire équilibrée en cuivre utilisée pour les communications en duplex intégral et l’alimentation de l’appareil connecté. Bien que le même câble puisse être réutilisé, l’émetteur-récepteur de communications de couche physique (PHY) et les composants passifs doivent être modifiés pour répondre à la norme 10BASE-T1L.
La validation de l’intégrité du signal 10BASE-T1L dans LTspice peut être, dans une large mesure, effectuée avec un signal de forme similaire.
Tableau 4. Portée d’une liaison Ethernet sur paire unique en fonction de l’amplitude du signal d’émission

Le codage utilisé est de type PAM36 (modulation d’impulsions en amplitude à 3 niveaux). En fonction de la portée souhaitée et des capacités des points d’extrémité, il est possible d’ajuster l’amplitude du signal d’émission sur 1 V ou 2,4 V.
Côté câble, la vitesse de montée du signal est de 53,33 ns pour une transition de -1 à +1 ; le temps de descente est identique.
La vitesse de balayage étant considérée comme constante, les transitions 0 à 1, 1 à 0, -1 à 0 et 0 à -1 doivent afficher un temps de transition nominal de 26,66 ns.
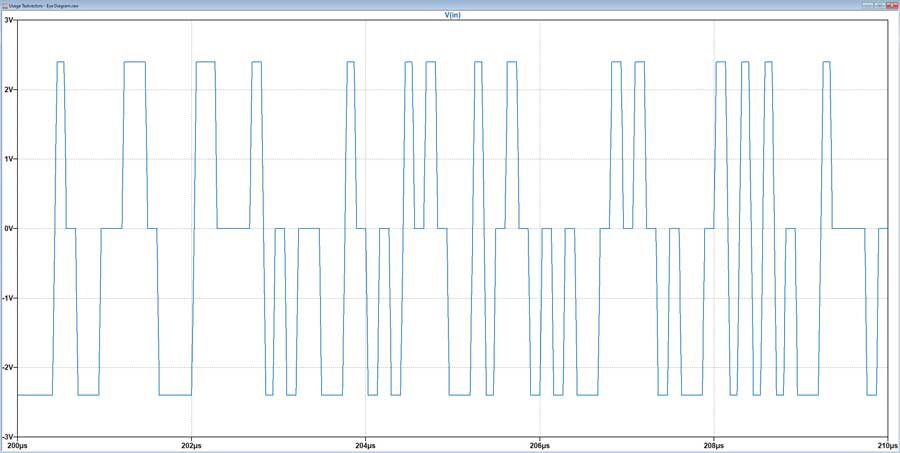
Pour générer un tel vecteur de test, nous utilisons le code de la figure?27P3, ce qui produira un vecteur de test de 5 000 symboles PAM3 au format PWL.
En injectant ce vecteur de test dans notre schéma, nous pourrons valider différents paramètres tels que le couplage minimum, la capacité entre enroulements, etc.

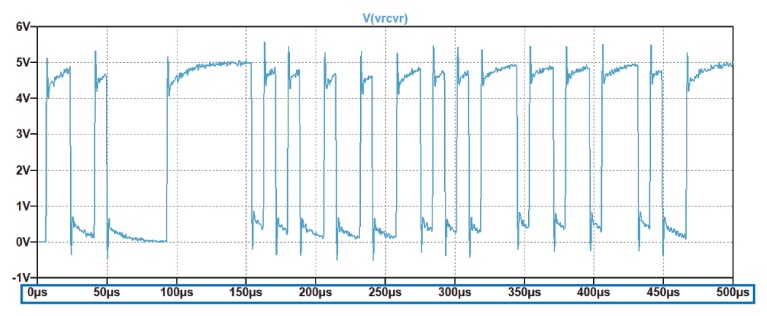
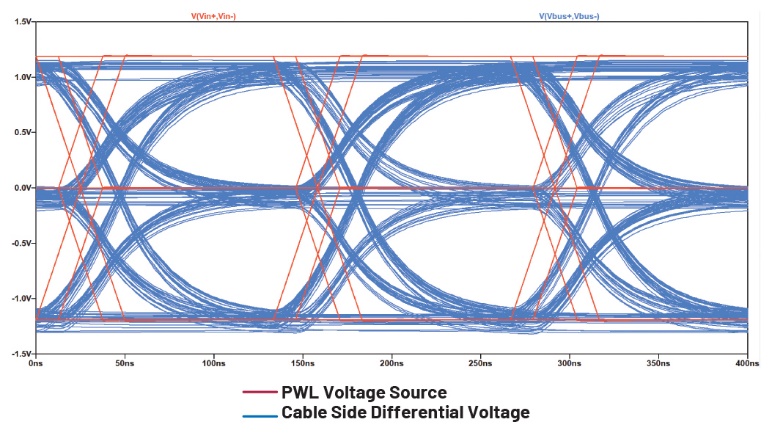
Les figures 28, 29 et 30 représentent la terminaison côté transformateur pour une liaison 10BASE-T1L, la sortie d’un fichier de tension source PWL et un diagramme de l’œil affichant la source de tension PWL et la tension différentielle côté câble. Ces valeurs peuvent être utilisées pour effectuer les tests de conformité à la norme 10BASE-T1L.
Conclusion
Disponible gratuitement, LTspice est un puissant logiciel de simulation qui peut être associé à des générateurs de formes d’onde en utilisant le langage C et du code JavaScript standard. Le résultat final est un outil haute performance de contrôle de l’intégrité des signaux de communications filaires qui permet d’accélérer les expériences en laboratoire, de guider la conception du produit final et de réduire les délais de mise sur le marché de nouveaux produits. ADI et Würth Elektronik mettront cet outil à la disposition concepteurs de liaisons câblées afin de les aider à maîtriser les nouvelles normes telles que 10BASE-T1L SPE.
Références
1. Signal Integrity Basics, livre blanc Signal Integrity, Anritsu, 2009.
2. Joseph Spencer et Gabino Alfonso. LTspice: Worst-Case Circuit Analysis with Minimal Simulations Runs, Analog Devices, Inc.
3. Steve Knudtsen. How to Model Statistical Tolerance Analysis for Complex Circuits Using LTspice, Analog Devices, Inc., août 2021.
4. Steffen Graber. 10 Mb/s Single Twisted Pair Ethernet, IEEE, mai 2017.
5. IEEE802.3-2022 clause 146 + annexe 146
6. IEEE802.3-2022 annexe 146A
Programmes?:
P1 C program generating simple randomized bitstream with limited consecutive 0 and 1
P2 HTML + Javascript generating eye diagram mask code for LTspice plot files
P3 C program generating randomized PAM3 bitstream
Source : com-trail.fr
